The law of Conservation of Mechanical Energy states that if no external forces act (or the work done by them is zero) and the internal forces are conservative, the mechanical energy of the system remains constant.
Struggling with Physics? Get online tutoring and homework help from the best Physics Tutor
What is conservation of mechanical energy?
The Law of Conservation of Mechanical Energy states that in a closed system where only conservative forces (such as gravity or spring force) are acting, the total mechanical energy of the system remains constant. This means that the sum of kinetic energy (K.E.) and potential energy (P.E.) remains unchanged over time, provided no external or non-conservative forces (like friction or air resistance) do work on the system.
What kind of question can we solve, and what kind of question can we not, using the law of Conservation of Mechanical Energy?
If non-conservative forces do work on the system or external forces do work on the system, we cannot use the conservation principle of total mechanical energy.
Suppose work done by non-conservative forces equals zero. In that case, work done by external forces equals zero, and internal forces operating within the system are conservative; then and only can we use the principle of conservation of total mechanical energy.
The law of Conservation of Mechanical Energy: Evidence through examples
Example 1: Freely falling object near the earth’s surface
Suppose a body of mass m is falling from rest near the earth’s surface. Initially (e = 0), it was at point A, at a height H above the earth’s surface.
Considering (earth + body) as a system and ground surface is considered a reference line. When the body is at point A, the total mechanical energy of the system is
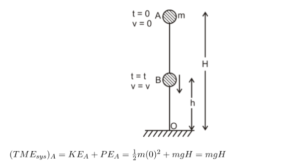
But at time t, the body reaches point B, the kinetic energy of the body increases, and the system’s potential energy decreases (because h < H). So, we see that the gain in the body’s kinetic energy is equal to the loss in potential energy of the system.
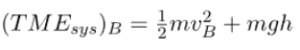
According to the principle of conservation of energy :
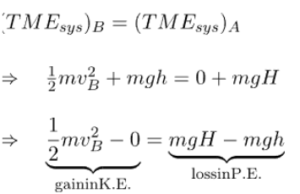
Example 2: A mass attached to a spring oscillating on a smooth surface
Consider a body moving with speed v0 on a smooth horizontal surface. As the body of mass m moves further, spring compresses. We are inserted to calculate the maximum compression produced in the spring.

Assuming block of mass m and spring as a system.
At the moment of maximum compression, the body’s speed becomes zero. Hence we see that the K.E. of the body decreases and the P.E. of the system increases.
So, loss in K.E. of the body is equal to gain in elastic potential energy.
According to the principle of conservation of TME.

The law of Conservation of Mechanical Energy: Equation
According to the work-energy theorem, as we know, the work done by all the forces equals the change in the kinetic energy.
Hence we can write,
![]()
Here, the three terms on the left denote the work done by the conservative internal forces, non-conservative internal forces, and external forces.
As we know, ![]()
Here, U stands for the potential energy of the system.
Now from (1) & (2),
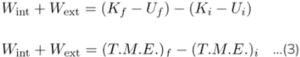
Where T.M.E. = K + U is the total mechanical energy.
If the internal forces are conservative but external forces act on the system and they do work, then from equation (3) we can write,
![]()
Therefore, we can write that the work done by external forces equals the change in the total mechanical energy of the system.
Here equation (4) is a mathematical form of energy conservation.
The Law of Conservation of Mechanical Energy: Solved Problems
Example 1: Finding work done by air friction
A body dropped from height h reaches the ground with speed . Calculate the work done by air friction.
In above question . Air friction is a non-conservative force. So, we cannot use the principle of conservation of total mechanical energy.
In this condition, we should use, work-energy theorem,
![]()
Example 2: Finding spring constant
A block of mass m moving at a speed v compresses a spring through a distance x before its speed is halved. Find the spring constant of the spring.
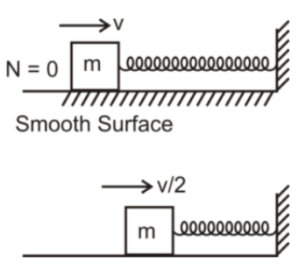
Let the system is (spring + block)
Here, ![]()
Internal force (spring force) is conservative.
So, we must use the principle of conservation of total mechanical energy.
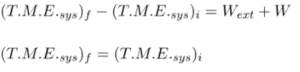
Because, in above example.
Example 3: Freely falling object, Speed and height calculations
A particle is released from height H. At a certain height from the ground, its kinetic energy is twice its gravitational potential energy. Find the speed of particles and height at that moment.
Ans: Considering particles and earth as a system;
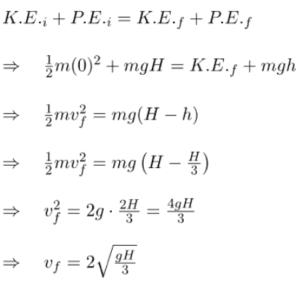
Also, ![]()
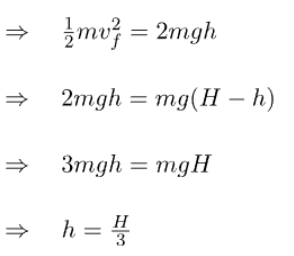
Example 4: Finding work done using the conservation of energy approach
Under the action of force, 2 kg body moves such that its position x varies as a function of time given by ; x is in meters, t is in second. Calculate the work done by the force in the first two seconds.
Ans: Considering 2 kg body and the earth as a system. Here, external force does work on the system,
Hence, we cannot use the energy conservation principle for this numerical.
So, here we will use work energy theorem,
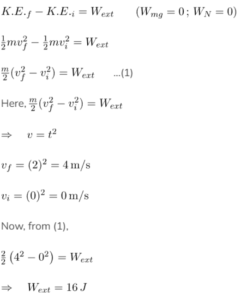
Still not sure about the law of conservation of mechanical energy?
My Engineering provides top Physics tutors who can help you learn and master it in a private 1:1 session. WhatsApp us to get started.
FAQs on the Law of Conservation of Mechanical Energy
1. What is the Law of Conservation of Mechanical Energy?
According to the Law of Conservation of Mechanical Energy, the sum of kinetic and potential energy, or total mechanical energy, stays constant in a closed system when only conservative forces are at work.
2. What are conservative and non-conservative forces in mechanical energy conservation?
- Conservative forces (like gravity and spring force) do not dissipate energy and allow energy to be fully recovered.
- Non-conservative forces (like friction and air resistance) cause energy dissipation, typically as heat or sound, leading to a decrease in total mechanical energy.
3. Why is friction considered a non-conservative force?
Friction is considered a non-conservative force because it converts mechanical energy into heat, which is lost from the system and cannot be fully recovered.
4. Can we apply the Law of Conservation of Mechanical Energy when friction is present?
No, the law only holds when non-conservative forces like friction and air resistance are absent or do no work on the system. If friction is present, mechanical energy is not conserved, and we must use the work-energy theorem instead.
5. How does the law apply to a freely falling object?
As an object falls under gravity, its potential energy (P.E.) decreases while its kinetic energy (K.E.) increases. However, the total mechanical energy (P.E. + K.E.) remains constant, assuming air resistance is negligible.
6. What is an example of mechanical energy conservation in real life?
A pendulum swinging back and forth is a perfect example. At the highest points, it has maximum potential energy and zero kinetic energy. As it swings down, potential energy converts into kinetic energy, keeping the total mechanical energy constant.
7. What happens to mechanical energy in a system with external forces?
If external forces (such as friction or applied forces) do work on the system, mechanical energy is no longer conserved. Instead, part of the energy is transformed into other forms, like heat or sound.
8. How does the law apply to an oscillating spring system?
Kinetic energy and elastic potential energy continually transform into one another in a mass-spring system when the mass oscillates. As long as the system is not subjected to non-conservative forces (such as friction), the total mechanical energy stays constant.
9. Why is the Law of Conservation of Mechanical Energy important in physics?
This law is an essential tenet of physics that aids in the resolution of issues pertaining to dynamics, motion, and energy transfer. By enabling us to equalize the starting and ultimate energy in a system, it streamlines computations in mechanics.
10. How is the Law of Conservation of Mechanical Energy used in problem-solving?
This law explains how energy flows between motion and position, which helps us calculate things like height and speed. In essence, it states that since total energy remains constant, we can forecast an object’s speed or altitude when it is falling or moving. This is quite helpful for things like springs, roller coasters, swings, and free-falling objects.

