Engineering students have long spent hours identifying the right equations, balancing force systems, or debugging complex thermodynamics models. Today, AI math solvers in engineering education are changing how these challenges are approached by offering structured, step-by-step computational support.
This shift does not eliminate effort it reshapes it. According to the National Academy of Engineering, mathematical modeling and problem-solving remain among the most critical competencies for future engineers. Educational platforms such as MIT OpenCourseWare also highlight how digital tools, when used responsibly, can strengthen conceptual understanding rather than replace it.
With tools like AI math solver GoMim, learners can visualize each stage of a calculation, check their logic, and deepen conceptual understanding through detailed step-by-step solutions. But how does AI truly fit into the landscape of real-world engineering problem-solving? Let’s explore how modern AI math solvers are transforming learning and professional practice in engineering.
The Role of Mathematics in Modern Engineering
Mathematics is the foundation of engineering. Civil, mechanical, electrical, and chemical engineering all rely on equations to model, analyze, and predict system behavior. From structural load calculations to control system design, mathematics translates physical reality into solvable models.
However, mastering this language is challenging. Students regularly encounter multivariable calculus, symbolic derivations, matrix algebra, and nonlinear systems. A small algebraic mistake can cascade into major errors in simulations or designs.
To understand the impact of this technology, let’s compare the traditional struggle of manual debugging against the workflow supported by AI tools.
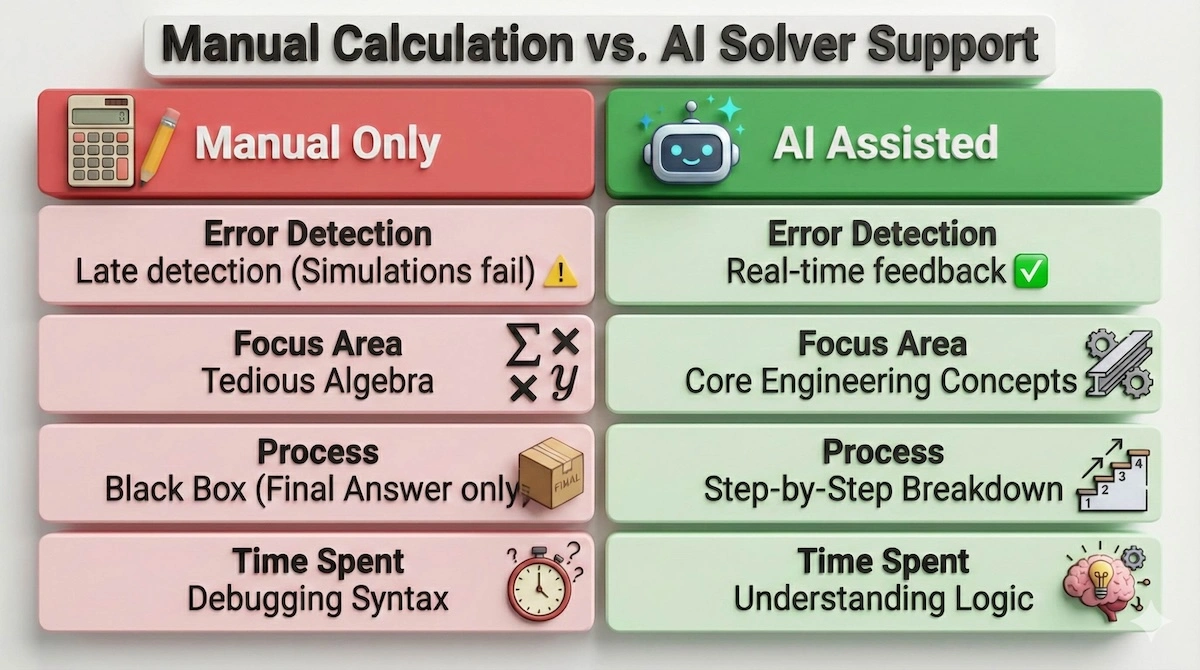
AI solvers shift the focus from tedious algebraic debugging to mastering core engineering concepts.
As the comparison shows, the primary shift is from spending time on error detection to focusing on core engineering logic.
AI math solvers help address this challenge by supporting comprehension and verification, not by replacing reasoning. Many tools now include image recognition and OCR capabilities, allowing students to input handwritten or printed equations accurately. This reduces friction while keeping the focus on understanding the math itself.
How AI Math Solvers Simplify Complex Calculations
Step-by-Step Learning Instead of Black-Box Answers
Unlike traditional calculators that return only final values, AI math solvers present intermediate steps. This allows learners to follow how equations evolve from setup and simplification to integration or transformation mirroring the reasoning process expected in engineering coursework.
This creates a ‘Glass Box’ learning loop where the process is transparent. Here is how you should structure your study workflow when using these tools:
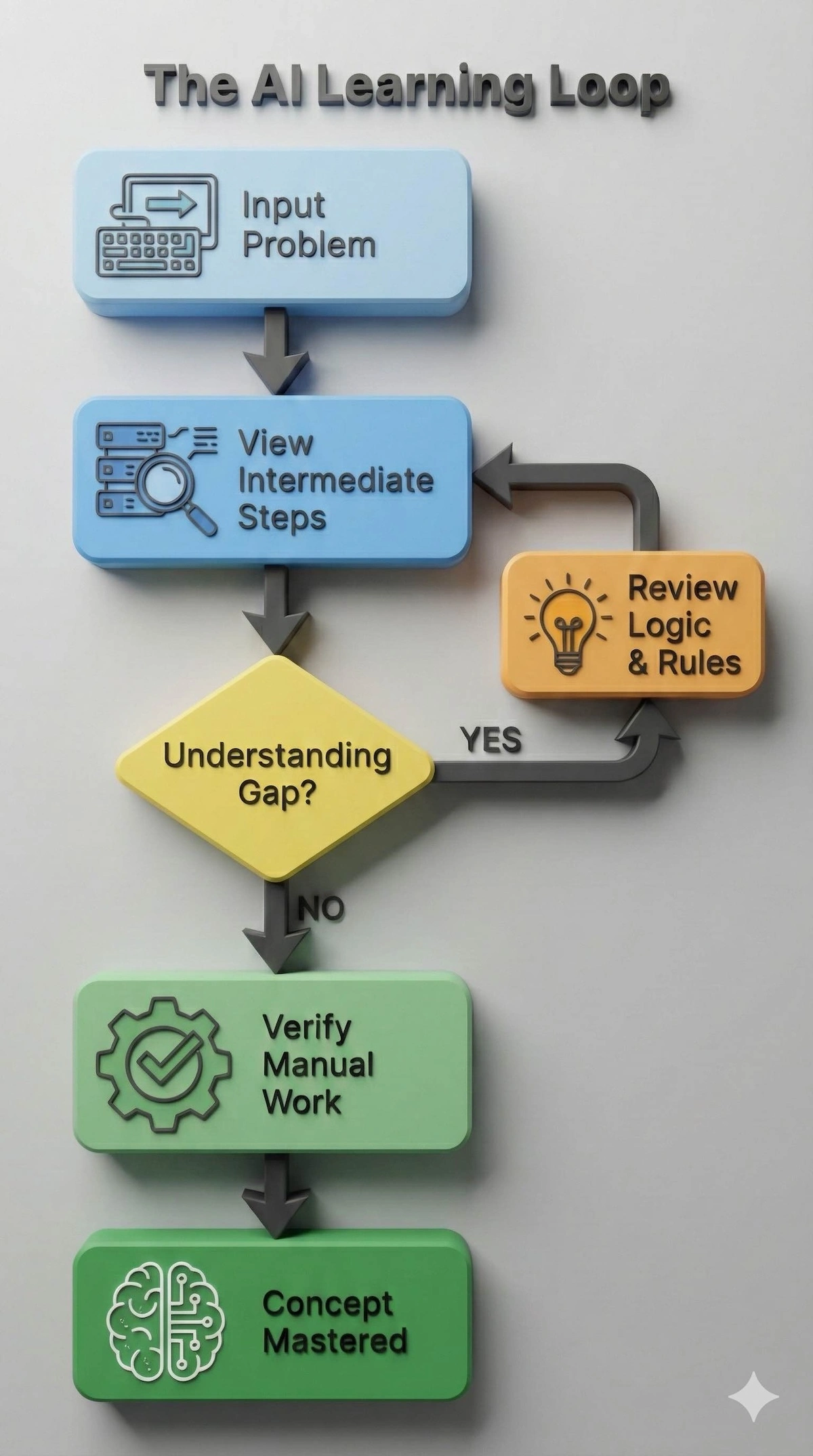
Instead of just copying answers, use the “Glass Box” method to review intermediate steps and bridge understanding gaps.
By following this loop, you ensure that every AI output becomes a verification step for your own work, rather than just a final answer.
This stepwise approach encourages active engagement rather than passive copying, making AI a learning aid rather than a shortcut.
Support Across Different Math Levels
One advantage of modern AI math solvers is adaptability. These tools can assist with:
- Basic algebra and trigonometry
- Multivariable calculus
- Linear algebra and differential equations
Explanations adjust to the user’s level, which makes them useful across undergraduate engineering curricula.
Real-Time Feedback and Error Detection
AI solvers also provide immediate feedback when errors occur. By flagging incorrect assumptions or algebraic slips early, students can correct misunderstandings before they become habits. This is particularly valuable for multi-step engineering problems where errors compound quickly.
Real Engineering Scenarios Supported by AI Math Solvers
-
Structural Load Analysis
One of the biggest hurdles for students is visualizing how a physical bridge translates into a grid of numbers. The diagram below illustrates this translation:
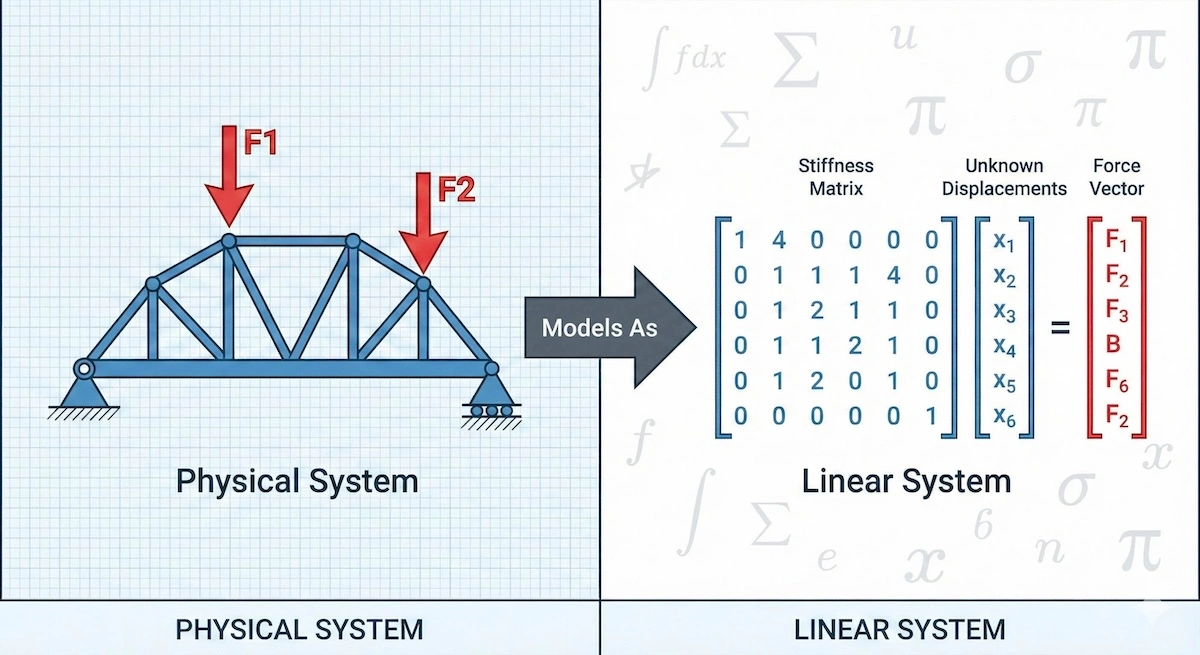
AI solvers excel at converting complex physical structures into solvable matrix equations, helping you visualize the math behind the metal.
While the physical structure (left) looks static, the mathematical model (right) allows engineers to predict exactly how it will behave under load.
Structural problems often reduce to systems of linear equations or matrix formulations. AI math solvers can walk students through equilibrium equations, matrix operations, and solution verification. While professional engineers rely on FEM software for real projects, AI solvers help students understand the mathematics underlying those tools.
-
Heat Transfer and Thermodynamics
Thermal analysis frequently involves partial differential equations. AI math solvers can demonstrate numerical methods, such as finite difference schemes, helping learners visualize temperature changes over time. These tools are effective for learning and quick validation, though final designs still require experimental data and specialized softwarware
-
Circuits and Signal Processing
In electrical engineering, transforms such as Laplace and Fourier methods are fundamental. AI math solvers can break down these transformations step by step, helping students understand relationships between time and frequency domains—an area where many learners struggle conceptually.
Visualizing a signal in two different domains simultaneously is difficult. The infographic below shows how AI tools instantly bridge the gap between Time and Frequency:
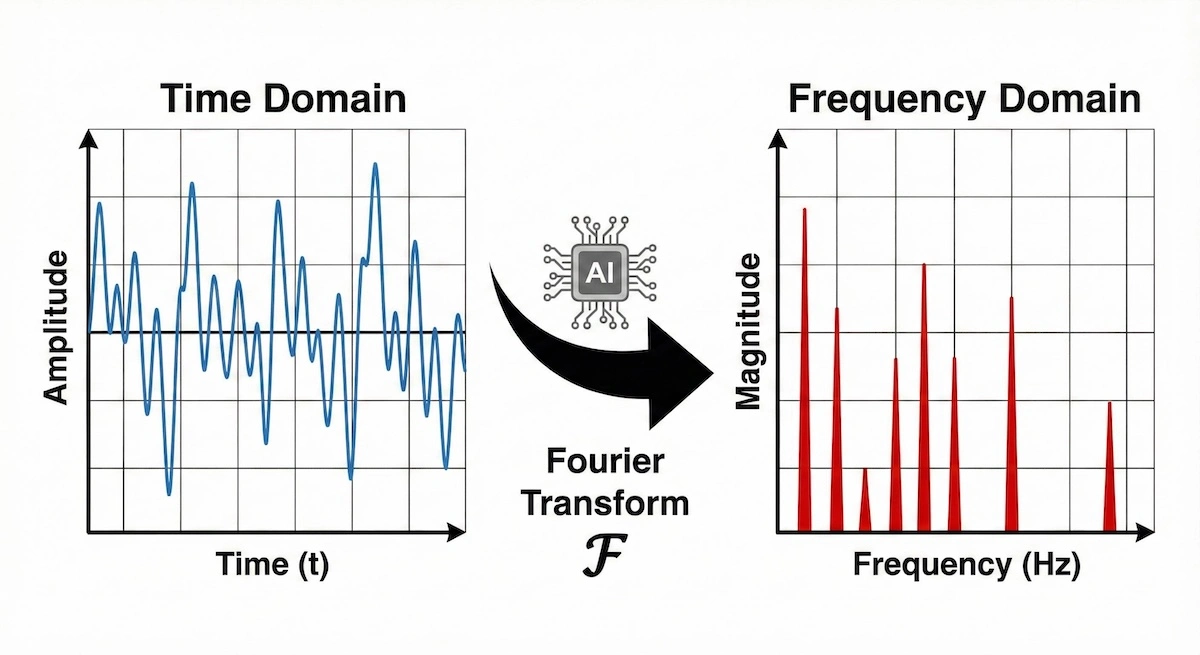
AI tools instantaneously visualize the relationship between complex time signals and their frequency components, a key concept in signal processing.
This transformation—often difficult to derive manually—becomes intuitive when you can see the waveform and its frequency spectrum side-by-side.
Benefits Beyond Quick Answers
The value of AI math solvers extends well beyond speed.
- Concept clarity: Step-by-step explanations reinforce derivations and physical meaning
- Error awareness: Immediate feedback highlights misconceptions early
- Skill scalability: Foundational understanding transfers to advanced topics such as control theory and fluid mechanics
- Better tutoring outcomes: Students who verify work independently arrive more prepared for guided sessions, including one-on-one academic support through platforms like MyEngineeringBuddy
Used correctly, AI solvers bridge independent study and human mentorship.
Real Engineering Scenarios Solved by AI Study Tool
To see how AI math solvers add value, consider their role across common engineering tasks.
Structural Load Analysis Example
In structural engineering, load and stress problems often reduce to systems of linear equations. An AI math solver like GoMim can help students and early-stage designers formulate these equations, walk through the matrix algebra step-by-step, and verify numerical outcomes on example problems.
Heat Transfer and Thermodynamics
Thermal analysis often involves solving partial differential equations such as the heat conduction equation. AI math solvers can demonstrate numerical approaches like finite difference schemes including the Crank Nicolson method helping users visualize how temperature evolves within a material. These functions, powered by AI and its OCR capabilities, are ideal for learning or rapid verification, though complex engineering designs still require specialized software and empirical validation.
Circuit and Signal Processing
In electrical engineering, tasks such as filter design and control-loop modeling rely on transforms and frequency analysis. AI math solvers can perform Laplace Transform or Fourier Transform steps on user-input functions, helping students comprehend the relationship between time and frequency domains.
Platforms such as the all-in-one learning tool Question AI provide step-by-step solutions and interactive tutoring spanning algebra, physics, and beyond bridging theory with practice in a student-friendly interface.
Practical Tips for Using AI Math Solvers Responsibly
- Attempt the problem manually first
- Use AI to verify intermediate steps, not just final answers
- Compare AI methods with classroom approaches
- Cite AI use transparently when allowed
- Follow institutional academic integrity guidelines
Unsure if you are using these tools ethically? Use this quick checklist before submitting any assignment:

Follow this checklist to ensure you’re using AI as a tutor, not a shortcut.
If you can check all the green boxes, you are using AI to enhance your education rather than shortcut it.
When used thoughtfully, AI strengthens learning rather than undermining it.
Conclusion
AI math solvers are reshaping how engineering students approach complex problems. By combining computational precision with structured explanations, they make advanced mathematics more accessible without removing the need for reasoning.
These tools do not replace human guidance. Instead, they complement mentorship by reinforcing understanding and preparing students for deeper discussions. When paired with academic support from platforms like MyEngineeringBuddy, AI-assisted learning becomes a powerful, balanced approach.
As engineering education evolves, success will depend not on avoiding AI but on using it responsibly to strengthen problem-solving, confidence, and real-world readiness.
FAQs on AI Math Solvers in Engineering Education
Are AI math solvers considered cheating?
Not inherently. They become problematic only when used to bypass learning rather than support it.
Can AI math solvers replace engineering software?
No. They assist with mathematical understanding but do not replace professional simulation tools.
Do AI math solvers help with conceptual understanding?
Yes, when they provide step-by-step explanations and students engage with the process.
Should students rely on AI before tutoring sessions?
Using AI for verification can make tutoring sessions more productive by highlighting specific gaps.
******************************
This article provides general educational guidance only. It is NOT official exam policy, professional academic advice, or guaranteed results. Always verify information with your school, official exam boards (College Board, Cambridge, IB), or qualified professionals before making decisions. Read Full Policies & Disclaimer , Contact Us To Report An Error

